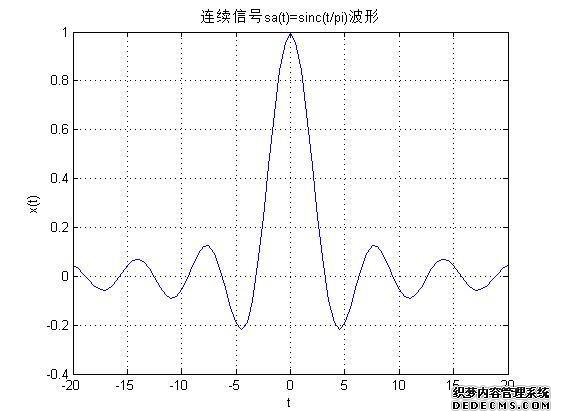
使用傅立叶变换对称性找到Sa(t)信号(大学信
作者:365bet体育注册开户 文章来源:365bet官方网投 发布时间:2019-09-30 23:30
全部展开δ(t)是单位脉冲响应。如果a趋于0,则当w = 0时F(jw)是无限的,而当w≠0时F(jw)是0,但这不是单位脉冲响应。
如果使用以下变换对,则傅立叶变换对具有多个定义:F(ω)=∫(∞,-∞)f(t)e ^(-iωt)dtf(t)=(1/2π)∫(∞,-∞)F(ω)e ^(iωt)dω命令:f(t)=δ(t),然后:∫(∞,-∞)δ(t)e ^(-iωt)Dt = 1和上一个公式的逆:(1 /2π)∫(∞,-∞)1e ^(iωt)dt =δ(t)/ /:狄拉克函数δ(t);因此,傅立叶变换常数等于:2πδ(t)扩展数据:摘要:假设采样频率为Fs且采样点数为N,则在FFT之后,以a表示的频率特定点n(n从1开始)是):Fn =(n-1)* Fs / N;将模块在这一点上除以N / 2,即相应频率下的信号幅度(NCC信号);在这一点上的相位为相应频率下的信号相位。
可以使用atan2(b,a)函数计算相位计算。
Atan2(b,a)是坐标为(a,b)的角度值,范围从-pi到pi。
为了获得xHz精度,您需要以1 / x秒的长度对信号进行采样并执行FFT。
增加频率分辨率需要增加采样点的数量,这对于某些实际应用而言不切实际,并且需要在短时间内完成分析。
解决该问题的方法是分频方法。最简单的方法是在短时间内对信号进行采样,添加一定数量的零,以使长度达到要求的点数,然后执行可能的FFT直到确定的点。改善。
细分的具体方法可以参考相关文献。
参考资料来源:百度百科-傅立叶变换