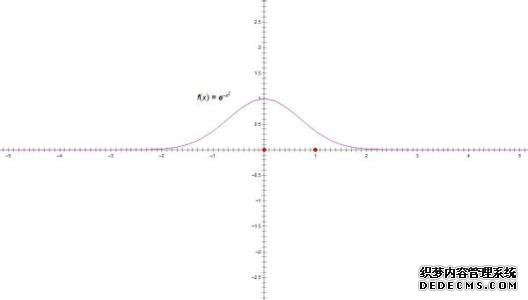
函数y = ex + e
作者:365bet比分网 文章来源:365bet平台注册 发布时间:2019-10-01 18:54
测试站点名称:功能域,价值域和价值域概念:参数值范围称为功能域,而功能值集称为功能值范围。
1.查找函数定义字段的一般方法如下:
(1)根据解析公式,如果偶数根类型的平方根大于零,则分母不能为零。(2)根据实际问题的要求确定自变量的范围。(3)需要根据相关分析表达式的域确定函数自变量的范围。(4)复数函数区域:如果y是u的函数,yu是x的函数,即y = f(u),u = g(x),y?? = f[g(x)]是一个函数它称为f和g的复合函数。u被称为中间变量。如果f(x)的区域为x∈M,而g(x)的区域为x∈N,则[当定义g(x)的区域时]为y = f。
使_ = f[g(x)]中的P区域。
3.函数值搜索方式范围:
(1)使用一些常用函数的单调性和值范围,例如一次性函数,二次函数,反比例函数,指数函数,对数函数,三角函数,形式函数(a,b是一个非零常数); 2)使用功能图像,即数字和格式的组合。(3)使用平均不等式。(4)使用判别式。(5)使用替换方法(三角变换等)。(6)分离方式:分离常数和参数两种形式。(7)使用复合函数的单调性。
(注意:闭合区间中二次函数值的范围需要特别注意对称轴与闭合区间之间的位置关系。在包含字符时请考虑自变量。)测试点名称:不平等基本应用及其基本不平等:
(仅当a = b时才使用符号“ =”)。变体:1(仅当a = b时才使用符号“ =”),即两个正数的算术平均值不小于其均值形状。
2; 3; 4;了解基本不平等:
(1)基本不等式的证明是通过重要不等式得出的。换句话说,有(2)个基本不等式,称为均值定理,平均不等式。这里,算术平均值,几何平均值和定理也可以解释如下:两个正数的算术平均值不小于那个几何平均值(3)建立不等式的条件和等式特别注意建立条件。对于平均值:1如果a = b,则取等号。也就是说,对于两个正数x和y,如果知道xy或x + y是固定值,则其余为:(1)如果xy = P(固定值),x = y则yx + y的最小值为2。(2)如果x + y = S(固定值)且x = y,则乘积xy具有最大值。(3)x2 + y2 = p,y x +是已知的,并且具有最大值。
应用基本不等式解决问题:
请注意,基本不等式适用并为建立等号(“一个正,两个固定,三相等”)创造了条件。
将实际大小与基本不平等进行比较。
(1)注意均值不等式的前提条件(2)使用均值定理使用元素加减法形成形式(3)注意用“ 1”代替(4)灵活地变换基本的不平等形式,并注意使用其变体形式。重要的不平等形式不仅支配原始形式,而且还可能,可能,可能的等等。(5)合理匹配,重复应用平均不平等。
基本不平等的一些变化: